What is Compression

In computing terms, Compression is representing a value with fewer bits than it normally is. Take the string "hello" for example, How is "hello" represented or stored in memory?

Firstly, we know the computer just knows 1's and 0's. With ASCII codes, every alphabet has a numeric representation, and then the number can be represented with at least 8 bits ¹. In Golang for example, to see the ASCII codes of the string "hello" as:

import "fmt"
fmt.Println([]byte("hello"))

This means every alphabet is represented with 8 bits (1 byte), so "hello" is represented with 5 bytes. After compression, the number of bytes that is used to describe "hello" should be below 5 bytes and at least a bit.

Generally, compressing very small values doesn't change much. This is why compression is mainly used for media that needs alot of bytes to be represented properly on the computer eg. videos, and raw audio files.

Compression aims to reduce the number of bytes sent over the wire, this increases speed and saves bandwidth.

In the diagram above, the original representation of "hello" is 4 bytes, but after compression, only 2 bytes are sent over the wire.

Lossy vs Lossless Compression

Compression algorithms can be lossy or lossless. lossy compression is a type of compression where the original value can't be gotten back from the compressed value. It's also called Irreversible compression. With Lossless compression, the original representation can be gotten from the compressed representation, and this is also called reversible compression.

Huffman Coding and Arithmetic Coding are examples of lossless compression algorithms while Transform Coding and Discrete Cosine Transform are lossy compression algorithms. The JPEG image format uses a lossy compression algorithm, and so if an image is compressed with this format, the original quality of the image can't be retrieved. PNG on the other hand, uses lossless compression. There are a lot of other lossless compression formats, Kraken, GZIP, Zlib etc.

Huffman Coding

Huffman Coding is a lossless compression algorithm with an elegant way of representing data. It simply works by ensuring the character with the highest frequency is represented with the smallest bits. This means for a string "how is henry having a hitch ?", the character "h" is the most frequent (excluding the empty spaces), and if it is represented with 2 bits instead of the usual 8 bits, then we have saved 6 bits for every occurrence of "h" in the string. This compresses the string significantly. Characters like "y" that appear sparingly will not be compressed as well as "h", or won't be compressed at all.

Huffman codes are prefix codes, this characteristic is of significant importance because it means that we can't have collisions, and there's no need for any extra synchronization when decoding or decompressing.

Implementation

Encoding / Compression

Using this text "how is henry having a hitch ?" as an example, the first thing to do will be to get the frequency of every single character in this string, and then sort it ² in ascending order and by frequency.

{
    "o":1, // smallest
    "r":1, 
    "s":1, 
    "t":1, 
    "v":1, 
    "w":1, 
    "y":1,
    "?":1,
    "c":1, 
    "e":1, 
    "g":1, 
    "a":2,
    "n":2,
    "i":3, 
    "h":5,  
    "":6, // highest
}

This is then heapified and represented in a priority queue, where the characters with the least frequency are at the top. At this point, every character is represented as a node. The character "h" should be a node with a value of "h" and a priority of 6:

type HuffmanNode struct {
    value string // "h"
    priority int // "6" this is the frequency
}

The Huffman tree is created by popping two characters with the least frequencies, adding their frequencies together, and then this new value should be pushed back to the queue. From the JSON object above, the two characters with the least frequencies are "o" and "r", so the tree should look like this:

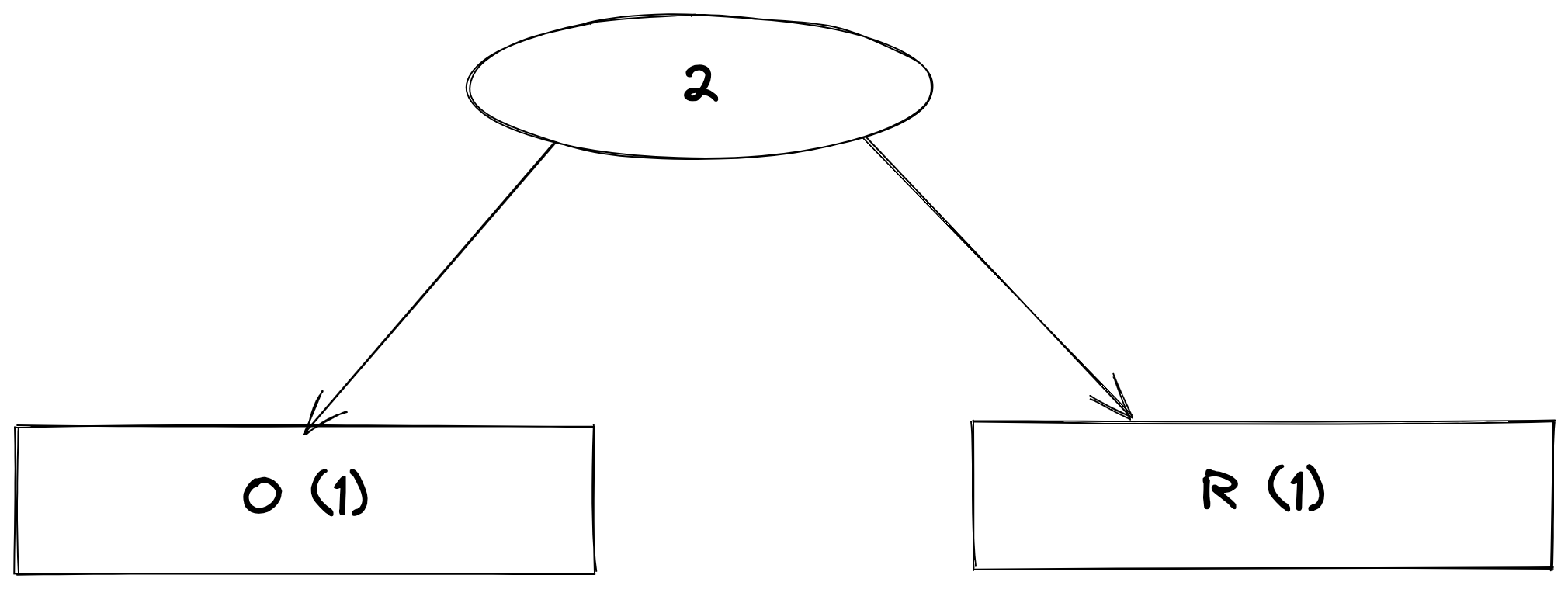
The leaf nodes are the only nodes with values in them and are represented with rectangles in the diagram, and the other nodes are internal nodes. These nodes just have a priority, no value. This process of popping, merging, and pushing back to the queue is repeated till the queue is empty.

When the tree is completed, a walk is done from the root to every leaf node, and if the path is left of the parent node then it's a "0" and if it's to the right of the parent node, then it's a "1".

From the example above, you can see that "A" is represented as "00" because it's left of its two parent nodes. Characters "A" and "B" are represented by only 2 bits each because they have higher frequencies of 7 and 5 respectively and "C", "D", "E" and "F" have more bits (3) because of lower frequencies.

Decoding / Decompression

The compressed bytes and the Huffman tree will be sent over the wire to the decoder, and the decoder will just recurse through the bits and when it hits a leaf node, it records the value, goes back to the root node, and walks a different path.

This proof of concept exists on Github, and I've run it for very large text files and on average, I achieve around 40% compression.

The time complexity for this is O(nlogn), where n is every distinct character in the string, and logn because a priority queue or min-heap is used to pop and push characters based on frequency. Multiple queues can be used to build the Huffman tree in O(n) time complexity.

Other variations of Huffman exist, for example, the n-ary Huffman coding and adaptive Huffman coding.

Huffman coding is not without its flaws, it's most optimal for input with a known probability distribution, if this isn't known, other algorithms like arithmetic coding can be used.

References

1. https://www.geeksforgeeks.org/huffman-coding-greedy-algo-3/
2. https://en.wikipedia.org/wiki/Huffman_coding#Applications
3. https://www.programiz.com/dsa/huffman-coding
4. https://engineering.purdue.edu/ece264/17au/hw/HW13?alt=huffman
5. https://www.sciencedirect.com/topics/engineering/huffman-code
6. https://iq.opengenus.org/huffman-decoding/